5 Régression polynomiale et régression spline

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

Exercice 1 (Questions de cours)  

  1. C
  2. A
  3. A
  4. B

Exercice 2 (Fonction polyreg)  

  1. On importe les données :

    ozone = pd.read_csv("../donnees/ozone_simple.txt", sep=";")
sdT12 = np.std(ozone['T12'], ddof=1)
print(sdT12)
    4.674638477781911

  2. On crée la grille

    grillex = np.linspace(ozone['T12'].min() - sdT12, ozone['T12'].max() + sdT12, 100)

  3. On transforme en data frame :

    df = pd.DataFrame({'T12': grillex})

  4. On effectue une regression polynomiale de degré 3 :

    basepoly = np.column_stack([ozone['T12']**i for i in range(1, 4)])
newval = np.column_stack([df['T12']**i for i in range(1, 4)])
dfpoly = pd.DataFrame(basepoly, columns=[f'T12^{i}' for i in range(1, 4)])
dfpoly['O3'] = ozone['O3']
X = sm.add_constant(dfpoly.drop(columns='O3'))
Y = dfpoly['O3']
regpoly = sm.OLS(Y, X).fit()
print(regpoly.summary())
                                OLS Regression Results                            
==============================================================================
Dep. Variable:                     O3   R-squared:                       0.536
Model:                            OLS   Adj. R-squared:                  0.505
Method:                 Least Squares   F-statistic:                     17.69
Date:                Sat, 01 Feb 2025   Prob (F-statistic):           8.92e-08
Time:                        18:01:00   Log-Likelihood:                -209.96
No. Observations:                  50   AIC:                             427.9
Df Residuals:                      46   BIC:                             435.6
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         69.2720     85.128      0.814      0.420    -102.081     240.625
T12^1          7.4578     14.405      0.518      0.607     -21.538      36.454
T12^2         -0.7730      0.784     -0.986      0.330      -2.352       0.806
T12^3          0.0208      0.014      1.519      0.136      -0.007       0.048
==============================================================================
Omnibus:                        2.509   Durbin-Watson:                   1.466
Prob(Omnibus):                  0.285   Jarque-Bera (JB):                1.745
Skew:                           0.251   Prob(JB):                        0.418
Kurtosis:                       2.235   Cond. No.                     4.15e+05
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.15e+05. This might indicate that there are
strong multicollinearity or other numerical problems.

  5. On prévoit sur lagrille :

    dfnewval = pd.DataFrame(newval, columns=[f'T12^{i}' for i in range(1, 4)])
dfnewval = sm.add_constant(dfnewval)
prev = regpoly.predict(dfnewval)
plt.scatter(ozone['T12'], ozone['O3'], label='Données')
plt.plot(grillex, prev, color='red', label='Prédictions')
plt.xlabel('T12')
plt.ylabel('O3')
plt.xlim(5,30)
plt.ylim(40,140)
plt.legend()
plt.show()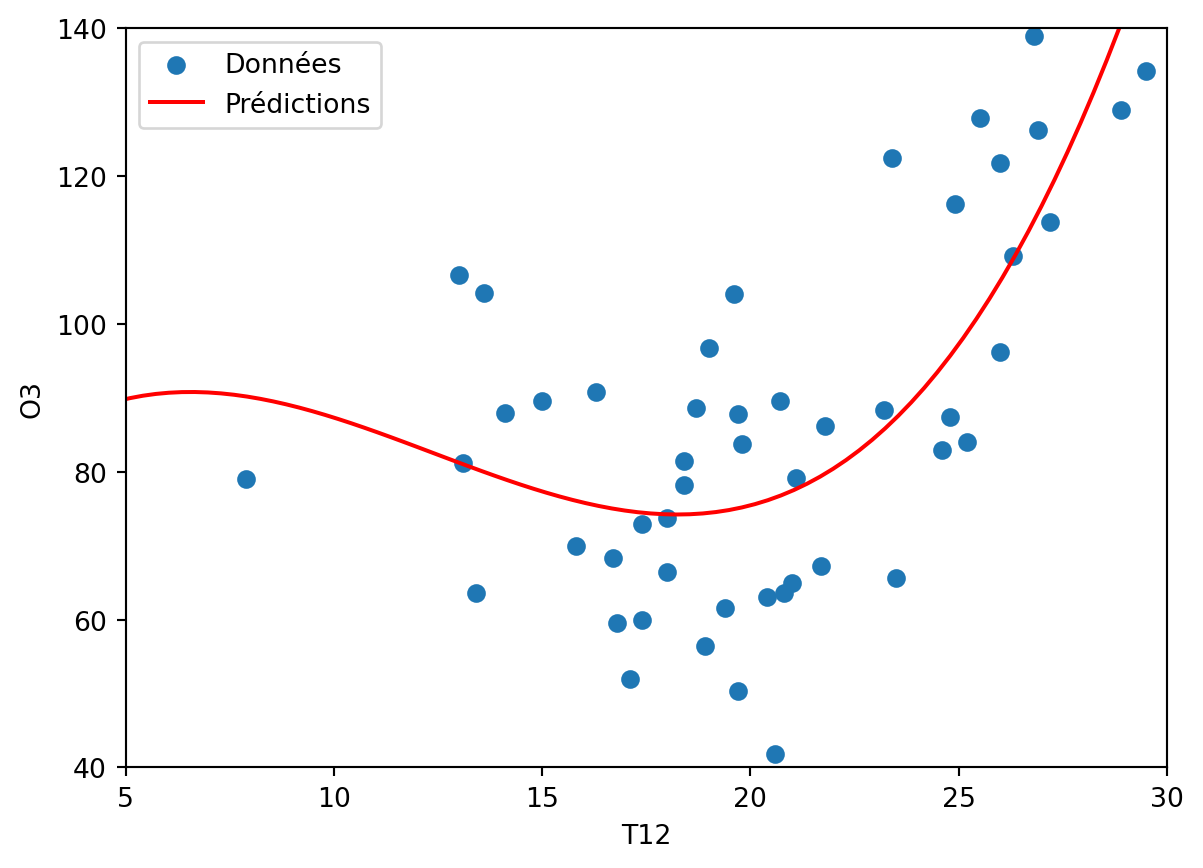

  6. Création de la fonction :

    def polyreg(ozone, degre=3):
    # Calculer l'écart-type de la colonne T12
    sdT12 = np.std(ozone['T12'], ddof=1)

    # Créer la grille
    grillex = np.linspace(ozone['T12'].min() - sdT12, ozone['T12'].max() + sdT12, 100)

    # Transformer en DataFrame
    df = pd.DataFrame({'T12': grillex})

    # Créer les termes polynomiaux de degré 3
    basepoly = np.column_stack([ozone['T12']**i for i in range(1, degre + 1)])

    # Prédire les nouvelles valeurs polynomiales
    newval = np.column_stack([df['T12']**i for i in range(1, degre + 1)])

    # Créer le DataFrame pour la régression
    dfpoly = pd.DataFrame(basepoly, columns=[f'T12^{i}' for i in range(1, degre + 1)])
    dfpoly['O3'] = ozone['O3']

    # Effectuer la régression polynomiale
    X = sm.add_constant(dfpoly.drop(columns='O3'))
    Y = dfpoly['O3']
    regpoly = sm.OLS(Y, X).fit()

    # Prédire les nouvelles valeurs
    dfnewval = pd.DataFrame(newval, columns=[f'T12^{i}' for i in range(1, degre + 1)])
    dfnewval = sm.add_constant(dfnewval)
    prev = regpoly.predict(dfnewval)

    return grillex, prev

Exercice 3 (Fonction polyreg (suite)) On applique la fonction précédente :

ozone = pd.read_csv("../donnees/ozone_simple.txt", sep=";")
# Tracer les données originales
plt.scatter(ozone['T12'], ozone['O3'], label='Données')
plt.xlim(0, 35)
plt.ylim(0, 150)
# Effectuer les régressions polynomiales et tracer les lignes
colors = ['blue', 'green', 'red', 'purple']
degrees = [1, 2, 3, 9]
for i, deg in enumerate(degrees):
    grillex, prev = polyreg(ozone, degre=deg)
    plt.plot(grillex, prev, color=colors[i], label=f'd={deg}')
# Ajouter la légende
plt.legend(loc='lower right')
plt.xlabel('T12')
plt.ylabel('O3')
plt.xlim(5,35)
plt.ylim(20,150)
plt.show()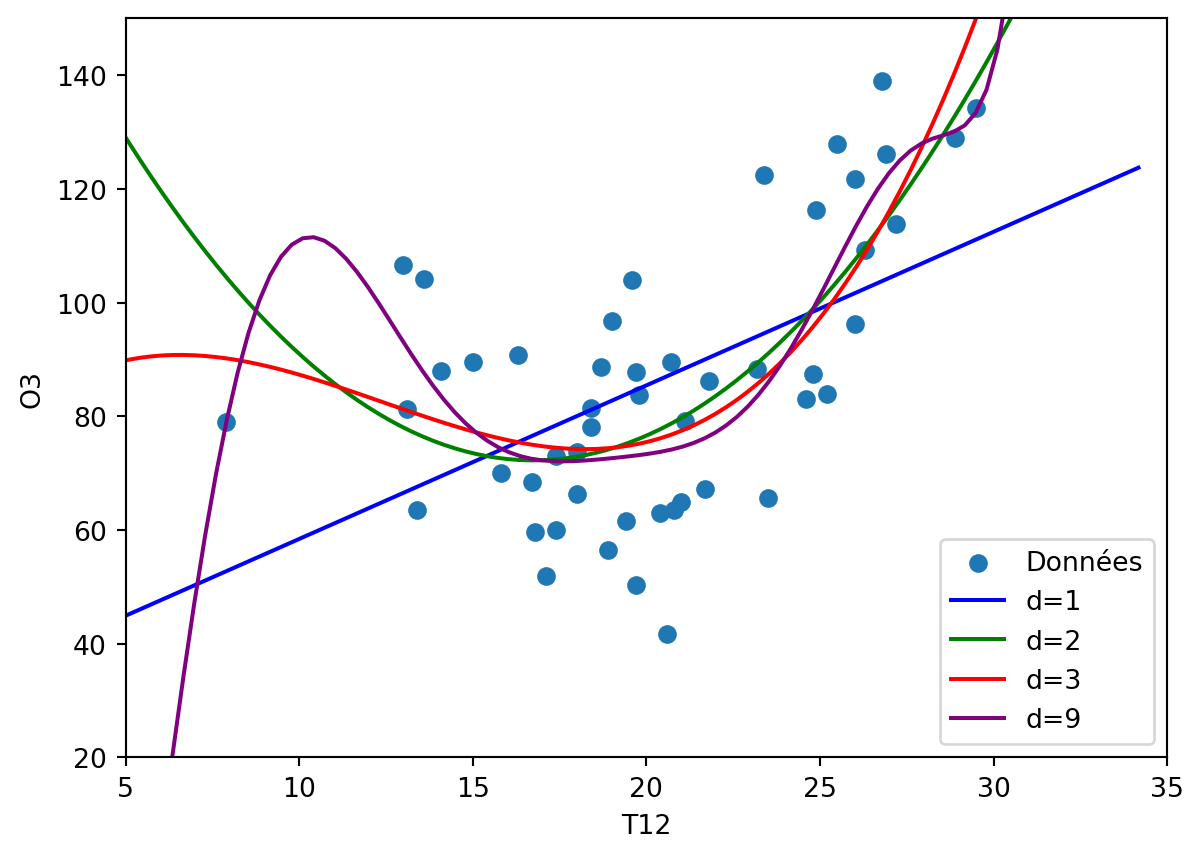

Exercice 4 (Matrice bande) Considérons la matrice \(X_B\) du plan d’expérience obtenue à partir d’une variable réelle \(X\) transformée dans \(\mathcal{S}_{\xi}^{d+1}\) . Cette matrice est composée des \(d+K+1\) fonction de base notée \(b_j\) et où \(K\) est le nombre de noeuds intérieurs et \(d\) le degré.

Dans le cours, il est indiqué que les fonctions de base \(b_j\) et \(b_{j+d+1}\) en conservant l’ordre des fonctions. Donc \(b_1\) est orthogonale à toutes les fonctions \(b_j\) avec \(j>d+1\), idem pour \(b_2\) avec \(j>d+2\).

En faisant donc le calcul \(X_B'X_B\) on obtient une matrice bande et donc les termes \(a_{ij}\) sont nuls quand \(j>i+d+1\).

On en déduit que les paramètres estimées \(\hat \beta_k\) ne sont pas corrélés avec les \(\hat \beta_j\) dès que \(j>k+d+1\). XB est une matrice bande.

Retour au sommet